
1. 개요
이번 문제는 2024년 국가직 7급 22번으로 출제되었던, 좌우 대칭 프레임의 절대 최대 휨모멘트를 구하는 문항입니다.
문제에서 “좌우 대칭인 라멘 구조물”이라는 문구를 굳이 언급한 이유는 출제자가 대칭 조건을 적극적으로 활용하라고 거의 직접적으로 힌트를 준 것입니다.
저는 과거 여러 기출 해설에서 강조했듯이, 구조물 대칭 + 하중 대칭 조건이 성립하면, 대칭축을 기준으로 구조물을 Fixed–Roller 모델로 치환할 수 있습니다. 이를 적용한 풀이 방식은 절점 수를 줄이고 자유도를 감소시키기 때문에 계산량이 극적으로 줄어듭니다. 이번 문제 역시 이러한 대칭 조건을 고려하면 실제로 상당히 간단하게 접근할 수 있습니다.
다만, 본 포스팅에서는 단순 해설에 그치지 않고, 대칭을 활용한 경우와 그렇지 않은 경우가 계산량과 풀이 효율에 어떤 차이를 만들어내는지 비교해보고자 합니다.
https://oreostructure.tistory.com/83
특히 예전에 설명드린 수정된 강성도(modified stiffness) 개념을 기억하신다면, 이 문제를 모멘트 분배법으로 풀 때 대칭 조건을 적용했을 때와 그렇지 않았을 때의 연산 과정이 얼마나 달라지는지 더욱 명확하게 느끼실 수 있을 것입니다.
수정된 처짐각 법 - 처짐각 법 pt 4 (연산을 가볍게)
1. 개요두 개의 회전각과 그에 대응하는 모멘트 사이의 관계식을 우리는 이미 여러 차례 도출해 보았습니다.또한 처짐 역시 현(Chord)–회전각으로 표현하여 모멘트와 연결하는 관계식도 정립해
oreostructure.com
정리하면 이번 포스팅의 목적은 다음과 같습니다.
- 대칭으로 인한 Fixed Roller 활용하지 않았을 때의 모멘트 분배법
- 수정된 강성도를 적용할 때 모멘트 분배법이 얼마나 간소화되는지 확인
이 과정을 통해, 시험장에서 어떤 전략을 선택해야 시간 효율·연산 안정성·정답률이 가장 높아지는지 명확하게 판단하실 수 있을 것입니다.
각각의 경우에 대해 빈 종이에 포스팅에서 다루고 있는 과정을 따라해보시기 바랍니다.
모멘트 분배법에 대한 감을 충분히 잡으시는데 큰 도움이 될 것입니다.
대칭으로 인하여 Sway =0 인 것은 계산상 편의를 위해 활용하도록 하겠습니다.
Sway가 없이 아래의 그림처럼 변형한다고 추정하는 것은 충분히 합리적입니다.
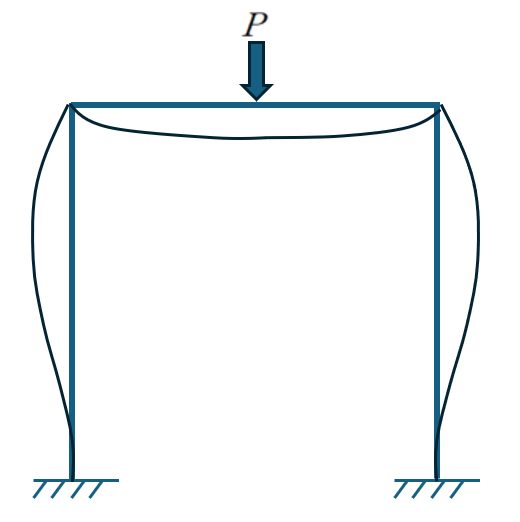
Sway가 있을때의 모멘트 분배법은 아래의 포스팅을 참고하시기 바랍니다.
https://oreostructure.tistory.com/89
2009년 7급 국가직 응용역학 4번 문제 (Sway 있을 때 모멘트 분배법)
1. 개요이전에 2009년 7급 국가직 응용역학 4번 문제에 대해 다음과 같은 풀이를 남긴 적이 있습니다.https://oreostructure.com/74 2009년 7급 국가직 응용역학 4번 문제 (등가절점하중 + 변위일치 해법)1. 개
oreostructure.com
2. 문제풀이 Ⅰ (대칭 : Fixed Roller 를 활용하지 않았을때)
Sway가 없으므로 해당 프레임 구조물은 3개의 연속된 보부재의 연결로 볼 수 있습니다.
꼭지점 B와 C는 부재 AB와 CD의 축변형이 없으며 Sway 변위가 없고 Rigid joint의 적합조건을 만족해야 하기 때문에
Roller (혹은 Hinge)로 취급 할 수 있습니다.

수정된 강성도를 활용하지 않을 것이므로 부재 AB와 BC, CD의 강성도는 모두 동일합니다. (동일 EI, 동일 부재 길이)
따라서 절점에 불균형 모멘트 발생시 이는 1:1의 비율로 나누어 갖게 됩니다.
시계방향 모멘트를 (clockwise moment) 양 (+) 값으로 취하겠습니다.
(1) 절점 B에서 불균일 모멘트 분배 : 1차
부재 BC에서 집중하중 P에 의해 작용하는 FEM은 -PL/8과 PL/8 입니다.

부재내 절점에 새롭게 추가되는 모멘트 발생시 반대편 부재에 1/2씩 Carry Over 를 해줍니다.
C절점에서 불균일 모멘트가 5PL/32 만큼 발생한 것을 확인 할 수 있습니다.
이것의 절반인 5PL/64만큼 차감하여 배분합니다.
(2) 절점 C에서 불균일 모멘트 분배 : 1차

Carry Over로 인하여 B절점에서 불균일 모멘트가 발생한 것을 발견하였습니다.
불균일 모멘트는 다음과 같습니다.
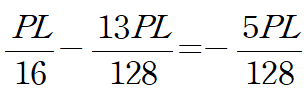
이것의 절반인 -5PL/256 만큼 각각 차감하여 재분배 합니다.
(3) 절점 B에서 불균일 모멘트 분배 : 2차

Carry Over로 인하여 C절점에서 불균일 모멘트가 발생한 것을 발견하였습니다.
불균일 모멘트는 다음과 같습니다.
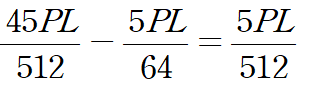
이것의 절반인 5PL/1024 만큼 각각 차감하여 재분배 합니다.
(4) 절점 C에서 불균일 모멘트 분배 : 2차
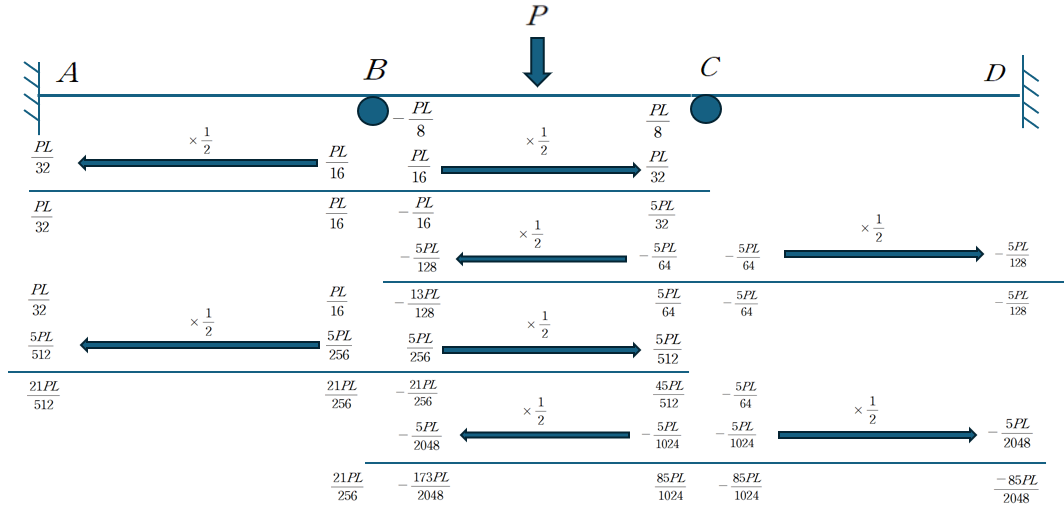
Carry Over로 인하여 B절점에서 불균일 모멘트가 발생한 것을 발견하였습니다.
불균일 모멘트는 다음과 같습니다.

이것의 절반인 -5PL/4096 만큼 각각 차감하여 재분배 합니다.
(5) 최종 결산

C 점의 모멘트 불균형은 5PL/8192 이며 이는 대략 0.00061PL 값입니다.
이것의 절반값은 5PL/16384 이며 대략 0.000305PL값입니다.
계속 모멘트 분배법을 하면서 불균형 모멘트로 인한 분배값을 되돌아보면
5PL/64 → -5PL/256 → 5PL/1024 → -5PL/4096 → 5PL/16384
순으로 지속적으로 작아졌습니다.
그렇게되면서 각 지점의 모멘트는 어떤 특정 값으로 수렴해가는 것을 확인할 수 있습니다.
비교하기 쉽게 소숫점으로 변환하여 이를 살펴보겠습니다.

근사적으로 대칭축을 기준으로 매우 유사한 값으로 수렴한 것도 확인할 수 있었습니다.
A점과 D점의 모멘트는 다음과 같습니다.

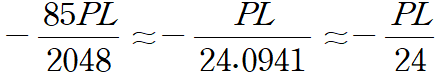
AB 부재에서 최대 모멘트는 B점에서 발생합니다.

대칭축 기준으로 반대편 모멘트를 살펴봐도 비슷합니다.

따라서 답은 ② 번이 되겠습니다.
매우 고통스럽고 힘든 과정을 거친 것 같습니다.
그렇다면 Fixed Roller를 활용하게 되면 어떻게 될까요?
2. 문제풀이 Ⅱ (대칭 : Fixed Roller 를 활용)
https://oreostructure.tistory.com/83
수정된 처짐각 법 - 처짐각 법 pt 4 (연산을 가볍게)
1. 개요두 개의 회전각과 그에 대응하는 모멘트 사이의 관계식을 우리는 이미 여러 차례 도출해 보았습니다.또한 처짐 역시 현(Chord)–회전각으로 표현하여 모멘트와 연결하는 관계식도 정립해
oreostructure.com
여기서 다뤘던 Fixed Roller의 강성도 값을 활용하겠습니다.
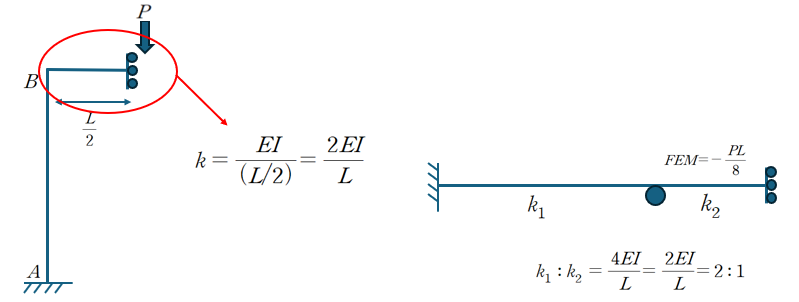
B점의 불균일 모멘트 -PL/8 을 강성도의 비율 2:1에 맞도록 분배합니다.
그리고 반대편으로 Carry Over 해줍니다.
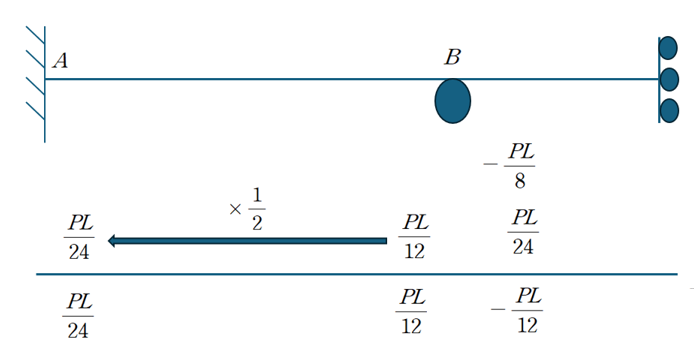
이번엔 근사치 해가 아닌 실제 해가 한번에 산정된 것을 볼 수 있습니다.
답은 B점에서 최대 모멘트 PL/12가 나오므로 ②번 입니다.
3. 마무리하며
비록 대칭 조건임에도 Fixed Roller를 활용하지 않고 계산을 진행하는 과정이 다소 고통스럽게 느껴질 수는 있지만, 모멘트 분배법의 원리를 몸으로 체득하기 위해 한 번쯤은 노가다에 가까운 계산 과정을 직접 경험해 보는 것도 충분히 의미가 있습니다.
빈 종이에 처음부터 직접 풀어 보아도 좋고, 제 포스팅을 띄워 둔 상태에서 하나하나 비교해 가며 따라 해도 좋습니다.
실제로 모멘트 분배법은 전산화된 구조해석 기법이 존재하지 않던 시절, 구조해석 실무에서 널리 사용되던 방법입니다.
다만 과거 다른 예제에서도 보았듯이 Sway가 존재하는 경우 계산량이 급격히 증가하며, 이번 포스팅에서 확인할 수 있듯이 대칭·역대칭 조건이나 모멘트가 0이 되는 지점에 대한 수정된 강성도를 활용하지 않는다면 계산량은 기하급수적으로 늘어나게 됩니다.
손계산이 전제되는 7급·9급 시험 환경에서는 연산량이 많다는 것 자체가 치명적인 약점이 됩니다.
따라서 수정된 강성도는 선택적으로 활용할 수 있는 기법이 아니라, 시험 대비를 위해 반드시 암기하고 능숙하게 적용해야 할 필수 요소라고 보아야 합니다.
'재미있는 문제- 쉬운풀이 > 모멘트 분배법' 카테고리의 다른 글
| 2018년 1차 서울시 7급 2번 (지점침하에 대한 응력법과 변위법 해석) (0) | 2026.02.02 |
|---|---|
| 2009년 7급 국가직 응용역학 4번 문제 (Sway 있을 때 모멘트 분배법) (1) | 2025.12.04 |