https://oreostructure.tistory.com/131
FEM 공식 유도 및 응용 (Ⅱ)
https://oreostructure.com/130 FEM 공식 유도 및 응용 (Ⅰ)안녕하세요. 오레오 구조입니다.이번 포스팅에서는 필수적으로 알아두어야 할 FEM(Fixed End Moment) 공식 몇 가지를 직접 유도해 보고,이를 실제 문제
oreostructure.com
안녕하세요. 오레오구조입니다.
이전 포스팅에 이어 FEM 공식 유도 내용을 계속해서 이어가고자 합니다.
이번 글에서는
일반적으로 구조기술사 수험생분들처럼 공학용 계산기를 활용하는 분들이 FEM을 유도하는 방식도 함께 소개해 보겠습니다.
참고로 말씀드리면,
공학용 계산기를 활용한 FEM 산정 자체는 매우 간단합니다.
대부분 최소일의 원리를 사용하기 때문입니다.
하지만 이 과정을 손계산으로 그대로 따라가려고 하면 상황이 완전히 달라집니다.
모멘트 방정식을 세우고, 이를 제곱한 뒤 적분하는 과정을 거쳐야 하며
연산량도 많고 실수 가능성도 매우 커집니다.
시험장에서 적용하기에는 상당히 부담스러운 방식입니다.
이번 포스팅에서는 다음 두 가지를 다룰 예정입니다.
- Case 5
: 최소일의 원리를 이용하여 FEM을 산정하는 방법 - Case 6
: 처짐각법을 활용하여 FEM을 산정하는 방법
Case 5는 실제로 종종 활용되는 케이스가 존재합니다.
반면 Case 6은, 이전 포스팅에서 다루었던 Case 4와 비교해 보면 개념이 훨씬 명확해질 것이라 판단되어 이번에 함께 다루게 되었습니다.
다만 이번 포스팅의 목적은
공학용 계산기를 활용하는 ‘스킬’을 가르치려는 것이 아닙니다.
Case 5와 Case 6 모두
이전 포스팅에서처럼 정정보의 양 끝단 처짐각을 먼저 계산한 뒤, 처짐이 0이 되도록 반력을 산정하는 방식으로도 충분히 쉽게 구할 수 있습니다.
즉, 굳이 최소일이나 복잡한 적분을 사용하지 않아도 되는 문제들입니다.
다만 누군가 “FEM은 최소일로 쉽게 구할 수 있어” 라고 말한다면,
그 말 속에는 반드시
‘(+ 공학용 계산기를 활용한다면)’
라는 말 숨어 있다는 점을 기억해 주셨으면 합니다.
7급 9급 시험장에서 필요한 것은
멋있어 보이는 이론이 아니라, 손계산으로 빠르고 안전하게 도달할 수 있는 풀이 전략입니다.
**참고로 제 공학용 계산기는 고장이 나서 새로 수리를 해야하는 상황입니다. 이에 따라 최소일 풀이 (Case 5에만 해당) 복잡한 각 과정을 모두 서술하기 보단 전반적인 커다란 플로우로 정리하도록 하겠습니다. 공학용 계산기가 있으신 분들은 계산기로 따라해보셔도 무방합니다.
다만 Case 5, Case 6 모두 이전 글과 같이 단순보 치환 → 회전각 산정 → 회전각 0으로 만드는 양단 모멘트 산정의 Flow로 방식으로 손계산만으로도 충분히 구할 수 있으니 꼭 풀어보시고 비교해 보시기 바랍니다.
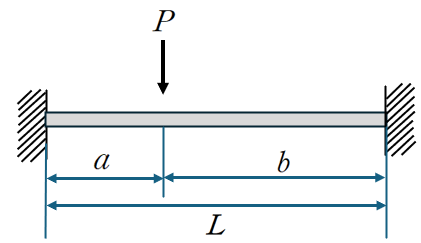
Case 5: 임의의 지점에서 집중하중 P가 작용할때 (최소일 풀이)
(1) 평형 방정식
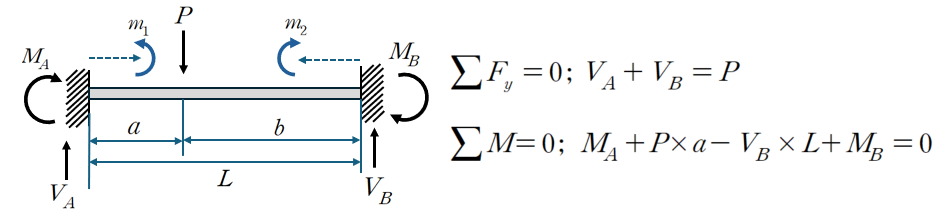
VB와 MB를 VA와 MA에 대해 표현하면
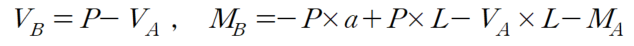
따라서 부재 내 모멘트를 산정하면 아래와 같습니다.
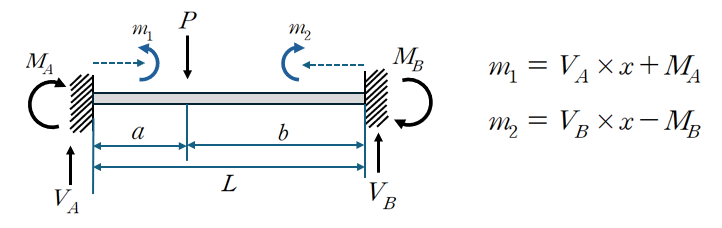
(2) 변형 에너지 산정 및 최소일
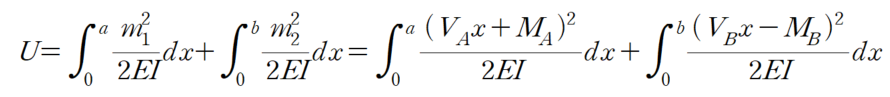
미지력은 변형에너지가 최소가 되도록 산정됩니다. 따라서,
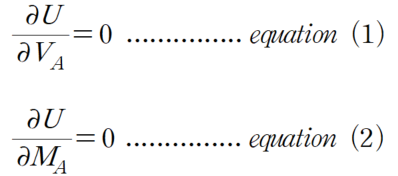
미지력 2개에 대한 2개의 방정식이 산정됩니다. 이를 풀어내면 다음과 같이 결과가 나옵니다.
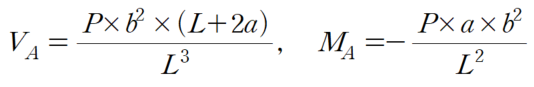
따라서 나머지 반력은 평형방정식에 대입시
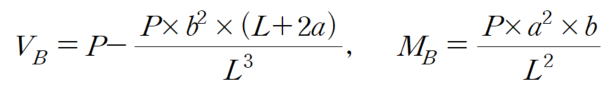
따라서 고정단 모멘트는 다음과 같이 정리할 수 있습니다.
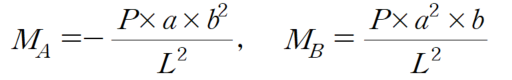
Case 6: 임의의 지점에서 집중모멘트 M이 작용할때 (처짐각법)
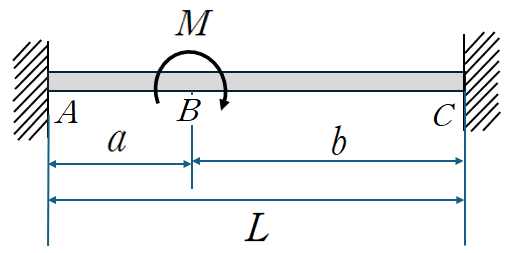
B점에서의 회전각 θ와 수직변위 δ로 부재력 표현 가능합니다.
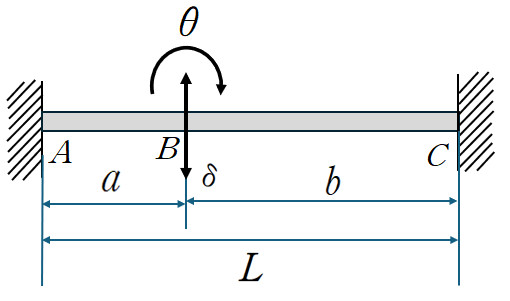
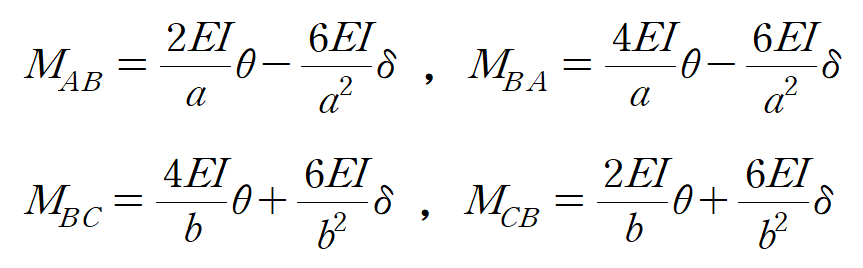
가상 변위의 법칙에 따라
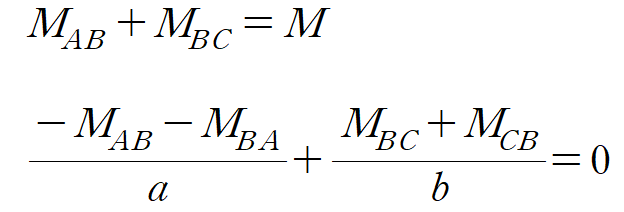
부재력을 대입하여 변위를 산정하게 되면
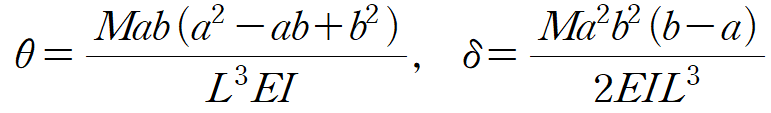
따라서 FEM에 해당하는 MAB와 MCB를 산정하면
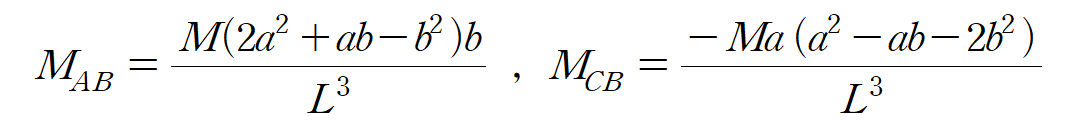
마무리하며
Case 5는 암기해야할 공식에 속하며 Case 6는 그렇지 않습니다.
다만 Case 6는 Case 4와 다르므로 잘못 이해하지 말자는 취지에서 산정하였습니다.
Case 6가 앞서 간단하게 Carry Over로 산정해낸 Case 4와 다른 이유는
첫째 역대칭이 아니며
둘째 수직 처짐이 발생하여 수직처짐에 따른 모멘트가 발생하기 때문입니다.
이에 대해 명확한 이해를 드리고자 산정한 것이며 참고로 비교하시면 될 것 같습니다.
'응용역학-구조역학 필수 이론' 카테고리의 다른 글
| FEM 공식 유도 및 응용 (Ⅱ) (1) | 2026.01.19 |
|---|---|
| FEM 공식 유도 및 응용 (Ⅰ) (2) | 2026.01.18 |
| 비틀림에 대한 이론 Ⅰ (원형 단면적을 갖고 있는 Shaft) (0) | 2026.01.12 |
| 수정된 처짐각 법 - 처짐각 법 pt 4 (연산을 가볍게) (0) | 2025.12.02 |
| 보 구조물 변위법의 기본 - 처짐각법 pt 3 (FEM 과 등가 절점 하중) (4) | 2025.11.12 |